We publish our first data on the Collatz function for 282589933 – 1 (#1 known megaprime) and two of its odd neighbors located at ±2.
Yearly Archives: 2019
Collatz function data for 2^77232917 – 1 (#2 known megaprime)
We publish our first data on the Collatz function for 277232917 – 1 (#2 known megaprime) and two of its odd neighbors located at ±4.
Collatz function data for 2^74207281 – 1 (#3 known megaprime)
We publish our first data on the Collatz function for 274207281 – 1 (#3 known megaprime) and two of its odd neighbors located at ±6.
Collatz function data for 2^57885161 – 1 (#4 known megaprime)
We publish our first data on the Collatz function for 257885161 – 1 (#4 known megaprime) and two of its odd neighbors located at ±8.
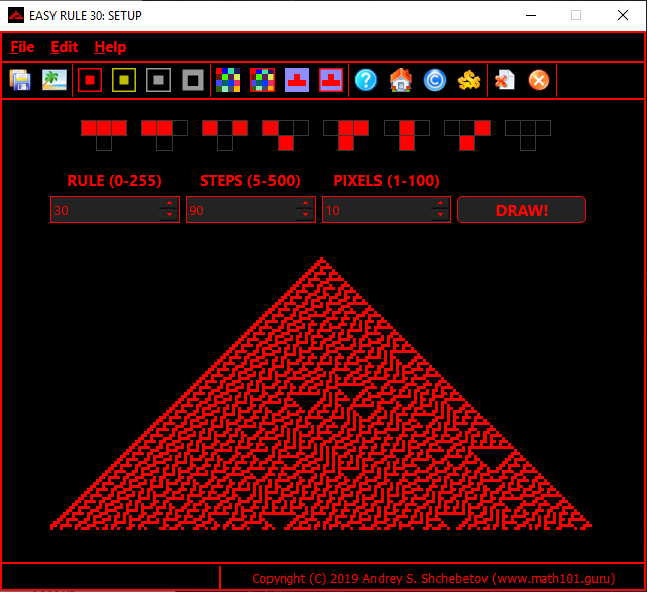
“Easy Rule 30” updated
Our “Easy Rule 30” was updated. You can download updated version through the following links:
Collatz function data for 2^43112609 – 1 (#5 known megaprime)
We publish our first data on the Collatz function for 243112609 – 1 (#5 known megaprime) and two of its odd neighbors located at ±10.
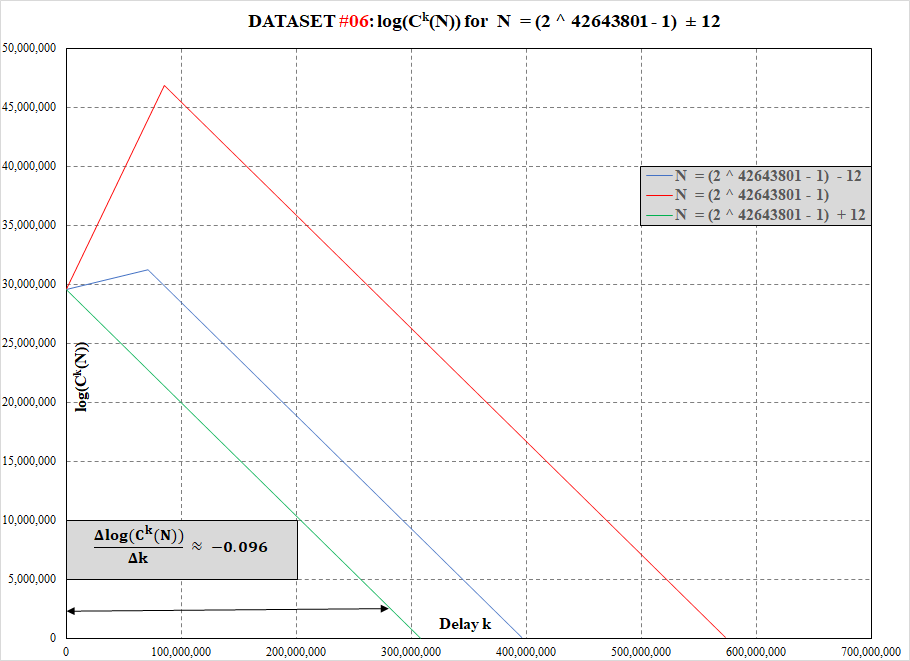
Additional Collatz function data for 2^42643801 – 1 (#6 known megaprime)
We publish further data on the Collatz function for 242643801 – 1 (#6 known megaprime) and two of its odd neighbors located at ±12.
Once the maximum is reached, the speed of decline for the log of the Collatz function seems to be the same for all tested numbers and is equal to approximately -0.096.
“Easy Rule 30” available for download
Collatz function data for 2^42643801 – 1 (#6 known megaprime)
We publish our first data on the Collatz function for 242643801 – 1 (#6 known megaprime) and two of its odd neighbors located at ±12.
“Easy Rule 30” software developed
On October 1, 2019 a well-known American mathematician Stephen Wolfram announced “Wolfram Rule 30 Prizes” science competition.
The competition is devoted to the solution of the so-called “Rule 30” – one of the unsolved math problems from a cellular automaton area.
Sequence of 19353600 record 288-step delayed palindromes published
Our sequence of 19353600 record 288-step delayed palindromes is published as A326414 .
The sequence starts with 12000700000025339936491 (the number discovered by Rob van Nobelen on April 26, 2019), ends with 29463993352000000700020 and contains all terms known at present.
Collatz function data for 2^37156667 – 1 (#7 known megaprime)
We publish our first data on the Collatz function for 237156667 – 1 (#7 known megaprime) and two of its odd neighbors located at ±26.
Collatz function data for 2^32582657 – 1 (#8 known megaprime)
We publish our first data on the Collatz function for 232582657 – 1 (#8 known megaprime) and two of its odd neighbors located at ±71149323674102624414.
Collatz function data for 10223×2^31172165 + 1 (#9 known megaprime)
We publish our first data on the Collatz function for 10223×231172165 + 1 (#9 known megaprime) and two of its odd neighbors located at ±4.
Collatz function data for 2^30402457 – 1 (#10 known megaprime)
We publish our first data on the Collatz function for 230402457 – 1 (#10 known megaprime) and two of its odd neighbors located at ±2.