We publish our first data on the Collatz function for 282589933 – 1 (#1 known megaprime) and two of its odd neighbors located at ±2.
Monthly Archives: December 2019
Collatz function data for 2^77232917 – 1 (#2 known megaprime)
We publish our first data on the Collatz function for 277232917 – 1 (#2 known megaprime) and two of its odd neighbors located at ±4.
Collatz function data for 2^74207281 – 1 (#3 known megaprime)
We publish our first data on the Collatz function for 274207281 – 1 (#3 known megaprime) and two of its odd neighbors located at ±6.
Collatz function data for 2^57885161 – 1 (#4 known megaprime)
We publish our first data on the Collatz function for 257885161 – 1 (#4 known megaprime) and two of its odd neighbors located at ±8.
“Easy Rule 30” updated
Our “Easy Rule 30” was updated. You can download updated version through the following links:
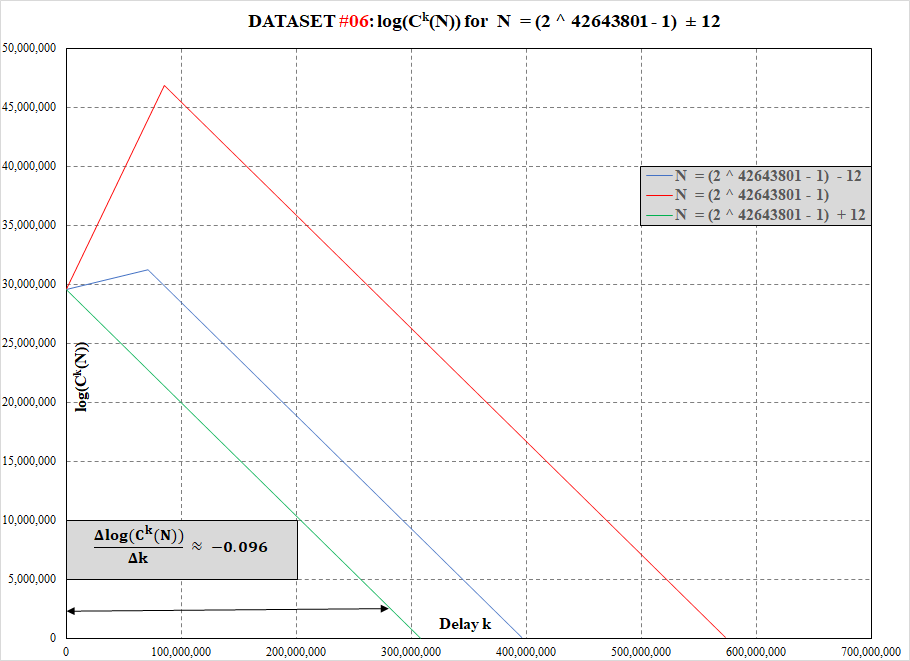
Collatz function data for 2^43112609 – 1 (#5 known megaprime)
We publish our first data on the Collatz function for 243112609 – 1 (#5 known megaprime) and two of its odd neighbors located at ±10.
Additional Collatz function data for 2^42643801 – 1 (#6 known megaprime)
We publish further data on the Collatz function for 242643801 – 1 (#6 known megaprime) and two of its odd neighbors located at ±12.
Once the maximum is reached, the speed of decline for the log of the Collatz function seems to be the same for all tested numbers and is equal to approximately -0.096.
