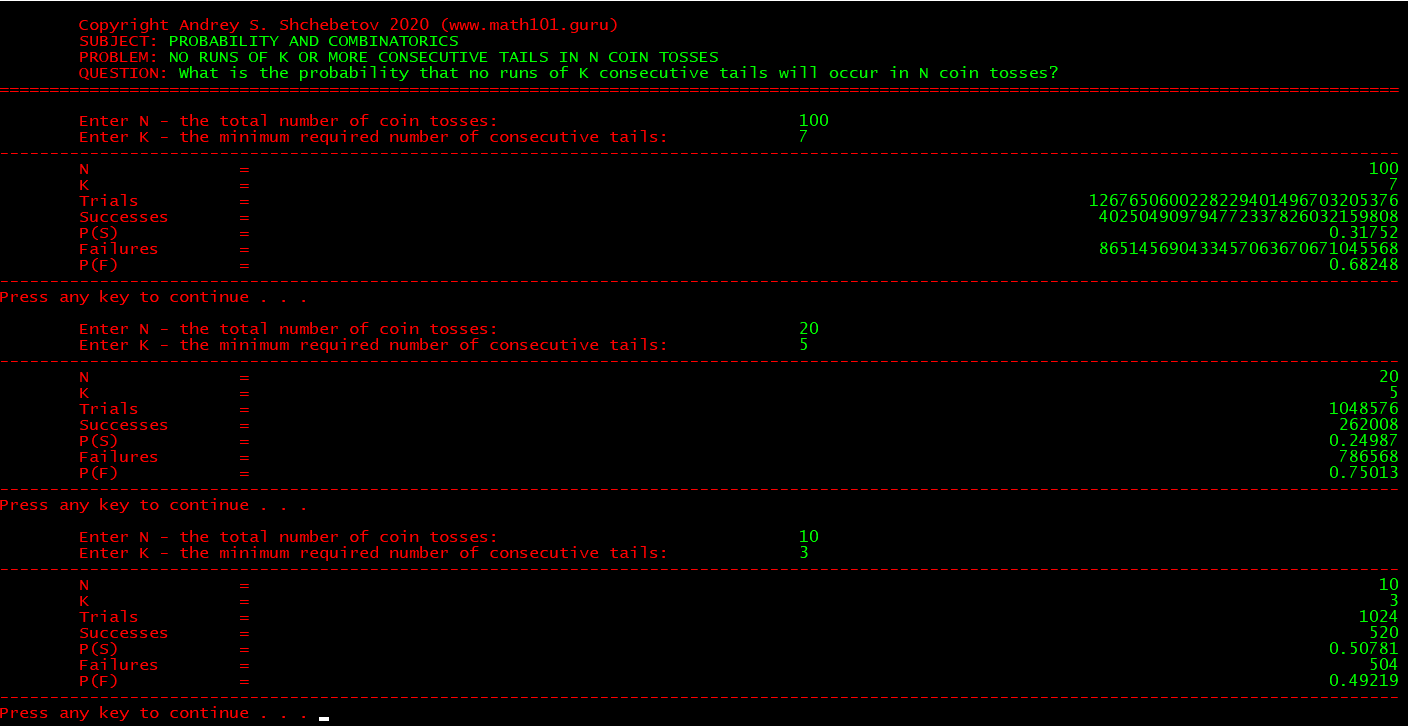
For my Probability and Statistics classes I wrote a small application that solves an old and  well-known problem: “What is the probability that no runs of K consecutive tails will occur in N coin tosses?”

This problem was first raised and solved by  Abraham de Moivre about 300 years ago. He calculated it for K = 3 and N = 10.

In 1937 a Stanford math professor James Victor Uspensky solved it in a modern way using generating functions. He also provided a numeric example for K = 5 and N = 20.

In 1960s William Feller provided an approximate solution presented in his famous probability book.

In 1980s the problem was solved again by several mathematicians using Markov chains.

In 2011 an American math student Benjamin Merkel solved it in his thesis using the set theory and provided a numeric example for K = 7 and N = 100.

You can download our application here (Windows 64-bit only). The application uses bignum arithmetic and works for any K and N. Enjoy!