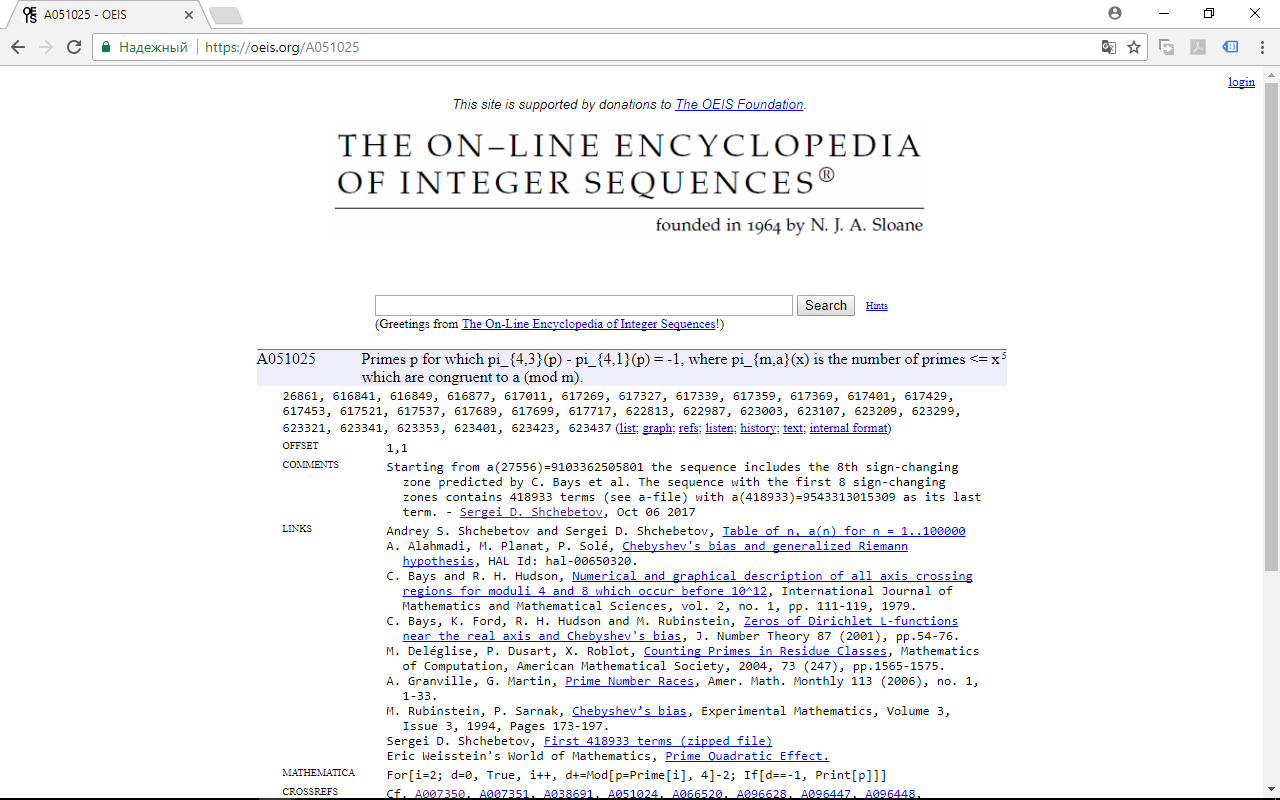
On October 6, 2017 we published in Online Encyclopedia of Integer Sequences (OEIS) under A051025 the full data on all 418933 primes where ∆{4;3,1}(x) becomes equal to -1. Staring from 27556th term equal to 9103362505801 the published sequence includes data on the 8th negative zone, that was predicted back in 2001 by a group of American mathematicians, but was never found.
The function ∆{4;3,1}(x) = π{4,3}(x) – π{4,1}(x) represents the difference between primes of the form 4k + 3 and primes of the form 4k + 1 up to a given x and plays important role in number theory. In 1853 the brilliant Russian mathematician Pafnuty Lvovich Chebyshev observed that this functions becomes negative quite rarely. Since then this phenomenon is known all over the world as Chebyshev’s bias. The direct numerical testing of this function present a complex and daunting computational problem complicated by inefficient algorithms, lack of memory and other limitations of modern computers.
The first seven sign-changing zones (including the negative ones) of this function were found between 1957 and 2001. The full data related to them has never been published before (e.g., OEIS A051025 contained just 30 terms). The 8th sign-changing zone was predicted back in 2001, but never actually found.
All our data available for download from OEIS as well as from our repository.
We plan to continue publishing our results on Chebyshev’s bias (including data on the narrow 9th sign-changing zone for ∆{4;3,1}(x), discovered by us) in the near future.