We are publishing the chart for DELTA{24,23,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.


We are publishing the chart for DELTA{24,23,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.

We are publishing the chart for DELTA{24,19,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.

We are publishing the chart for DELTA{24,17,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.

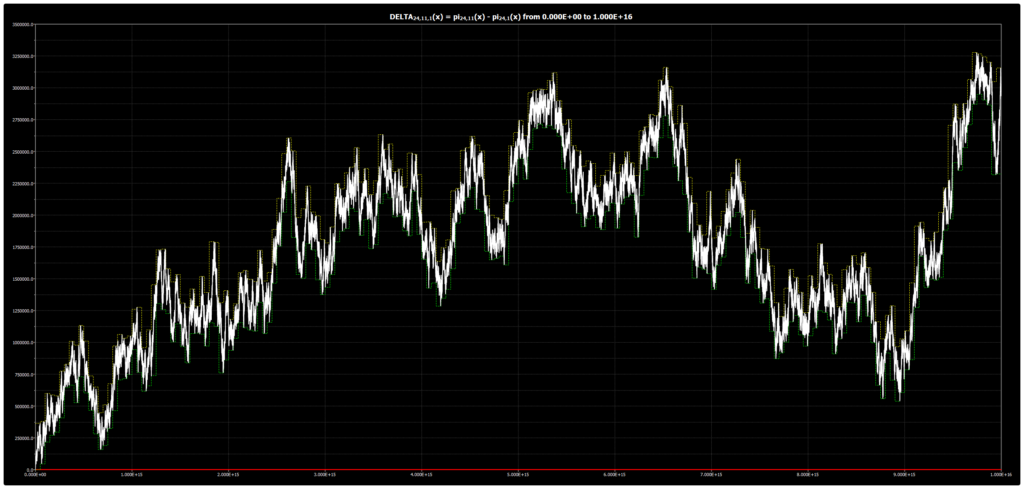
We are publishing the chart for DELTA{24,13,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.

We are publishing the chart for DELTA{24,11,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
We are publishing the chart for DELTA{24,7,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.

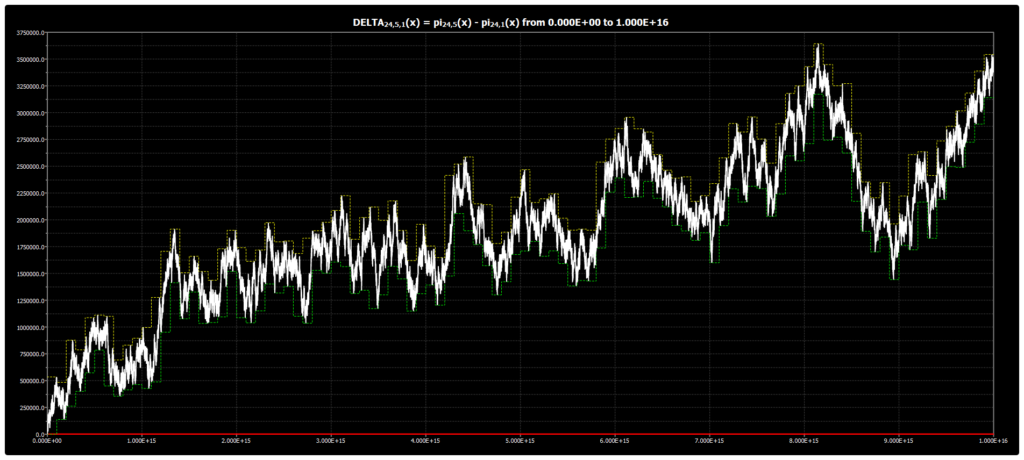
We are publishing the chart for DELTA{24,5,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
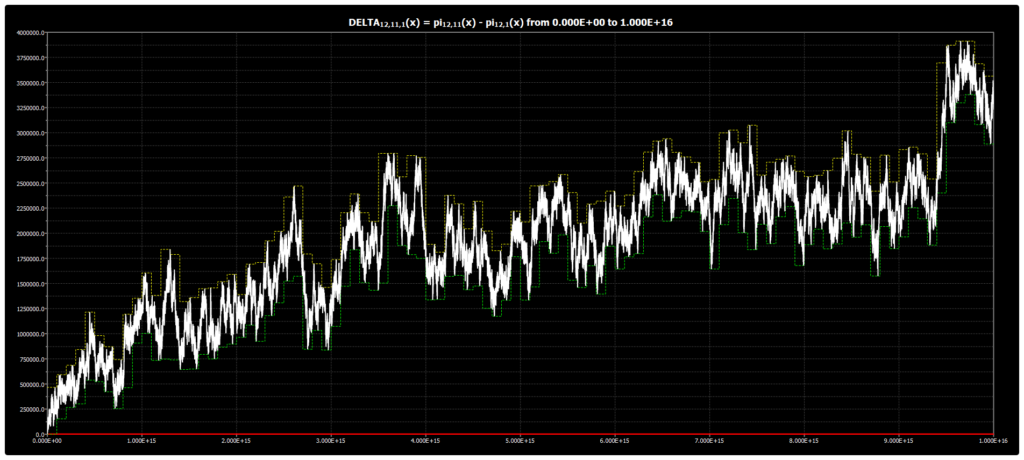
We are publishing the chart for DELTA{12,11,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
We are publishing the chart for DELTA{12,7,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.

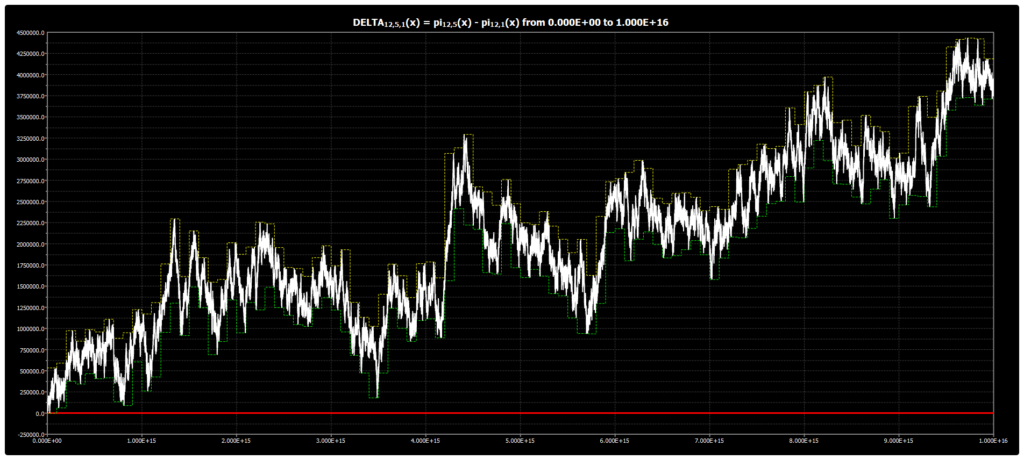
We are publishing the chart for DELTA{12,5,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
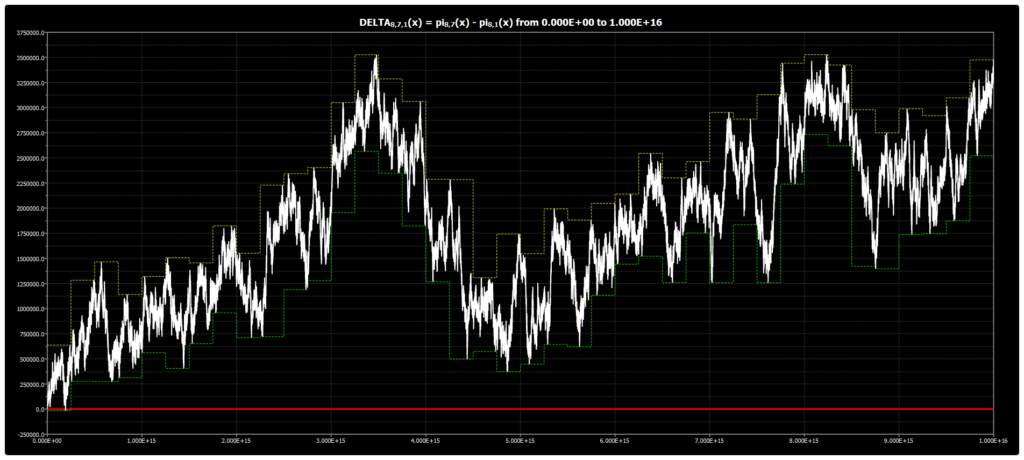
We are publishing the chart for DELTA{8,7,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
We are publishing the chart for DELTA{8,5,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.

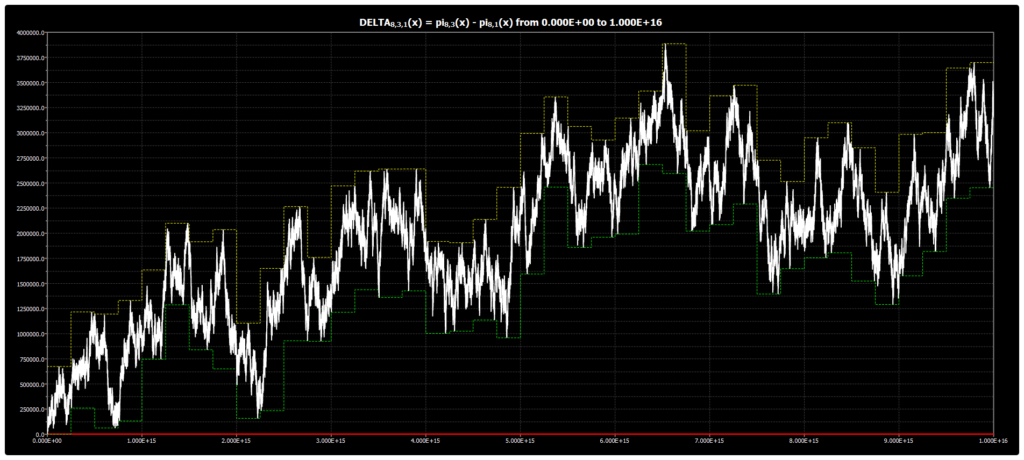
We are publishing the chart for DELTA{8,3,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
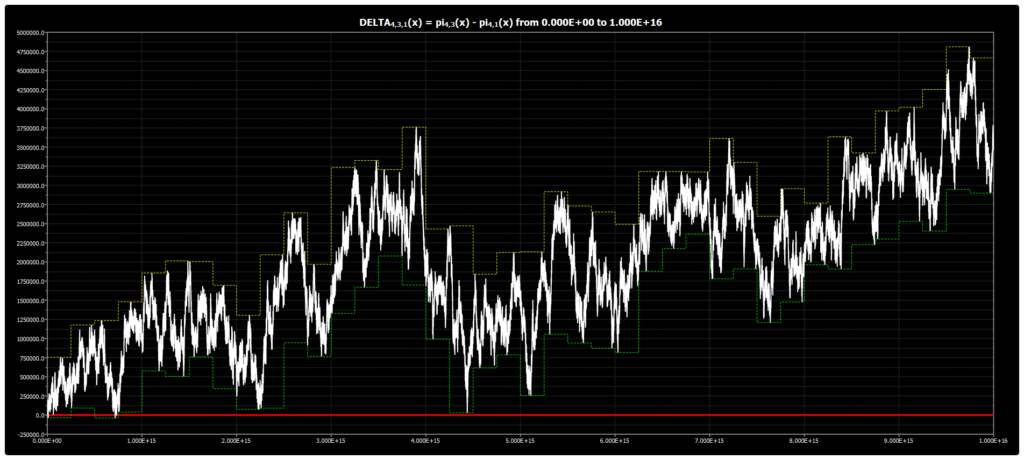
We are publishing the chart for DELTA{4,3,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
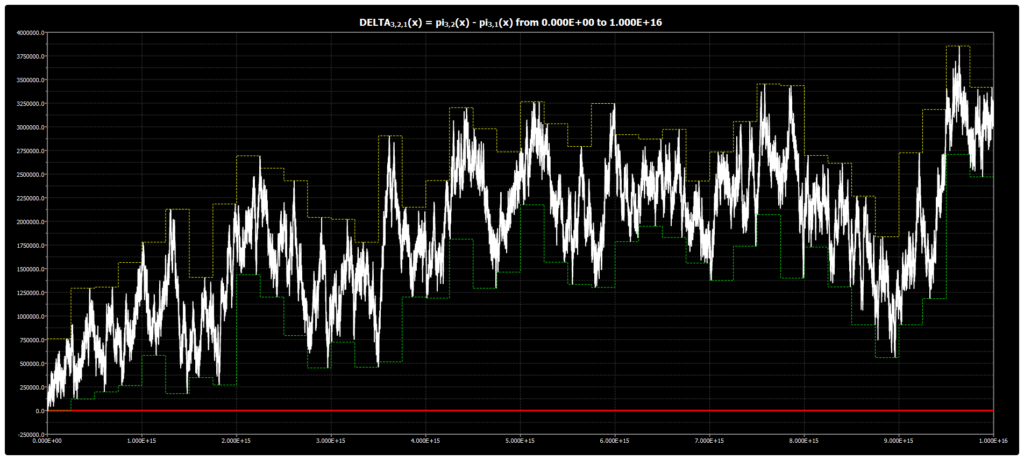
We are publishing the chart for DELTA{3,2,1}(x) up to 1016 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.