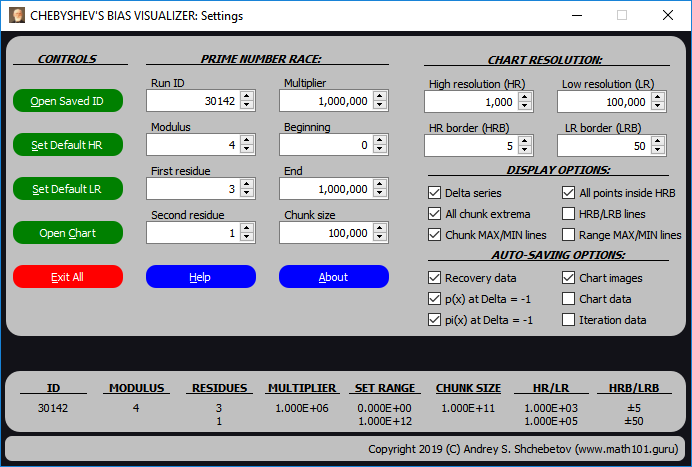
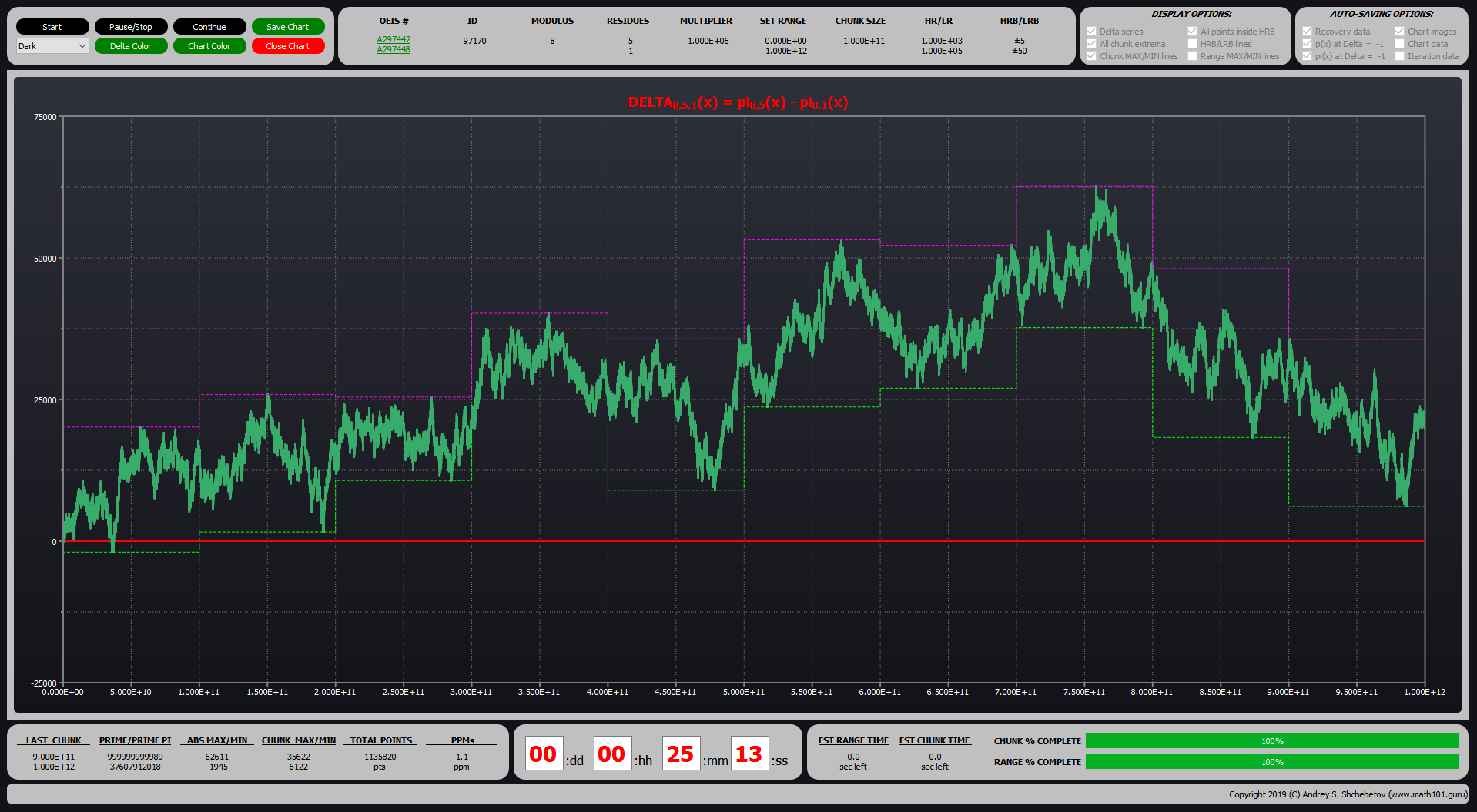
Мы выпускаем вторую версию «Chebyshev’s Bias Visualizer» — программы, которая позволяет наглядно продемонстрировать математический феномен открытый более 165 лет назад блестящим российским ученым Пафнутием Львовичем Чебышёвым и связанный с Обобщенной гипотезой Римана.
Вторая версия программы имеет улучшенный пользовательский интерфейс и ряд новых функций, включая возможность перемещения по графику и его увеличения или уменьшения.
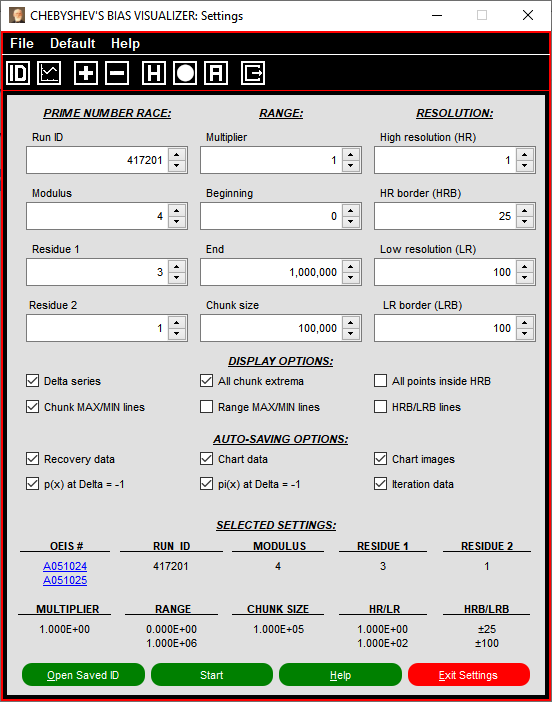

Вы можете загрузить новую версию для Windows 64-bit по следующей ссылке: cbv_win64_setup.
Версии для других платформ будут выпущены позже.