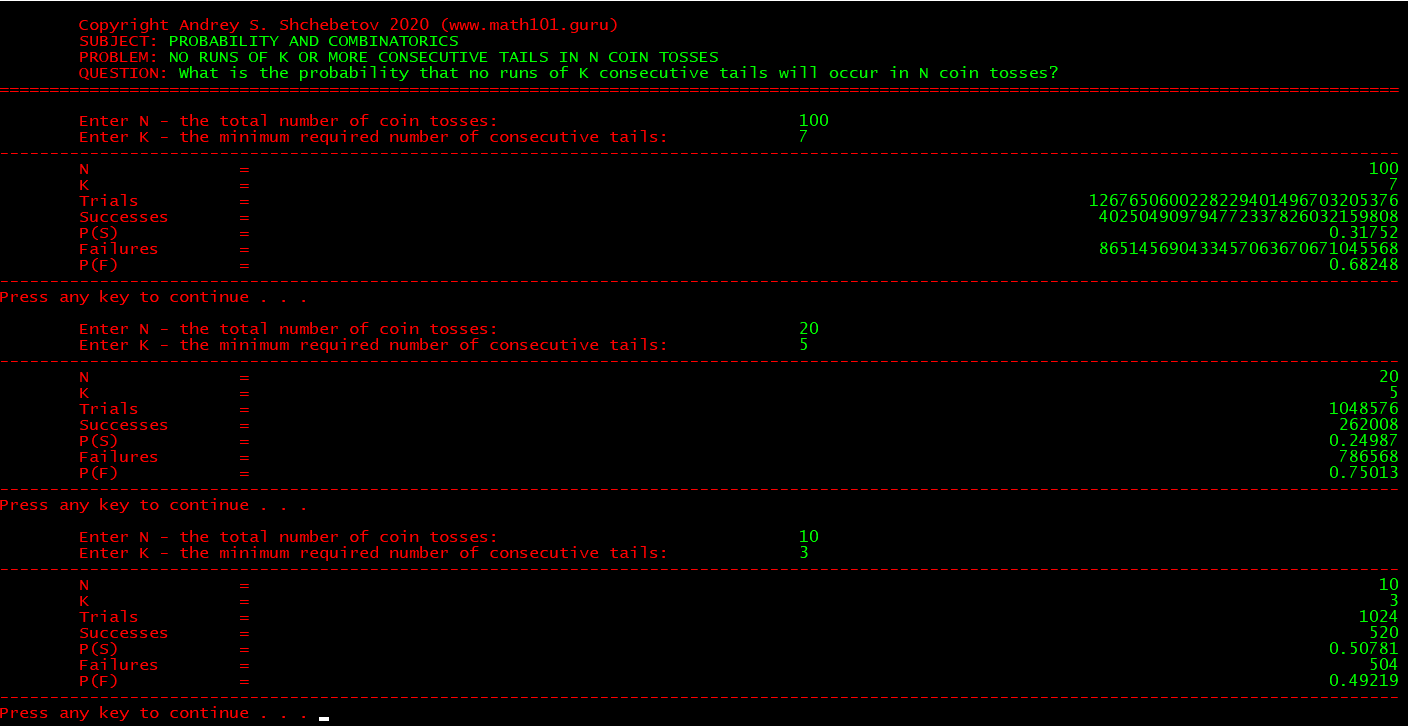
Для своего курса по теории вероятностей и математической статистики, я написал небольшую программу, котороя решает старую и хорошо известную задачу: “Какова вероятность того, что про N бросках монетки не выпадет K орлов подряд?”

Впервые эта задача была сформулирована и решена Абрахамом де Муавром более 300 лет назад. Он также посчитал вероятность при K = 3 и N = 10.

В 1937 году профессор математики Стэнфордского Университета Яков Викторович Успенский решил данную задачу современным способом с помощью генерирующих функций. Он также представил численный пример для K = 5 и N = 20.

В 1960х годах эта задача была решена асимптотически Вильямом Феллером и изложена в его знаменитой книге по теории вероятности.

В 1980х годах эта задача снова была решена несколькими математиками с использованием цепей Маркова.

В 2011 году американский студент-математик Бенджамин Меркель решил эту задачу в своей дипломной работе с помощью теории множеств, а также представил расчет для K = 7 и N = 100.

Вы можете загрузить наше приложение здесь. Приложение использует длинную арифметику с целыми числами и работает для любых значений K и N. Наслаждайтесь!