We are publishing the chart for DELTA{24,13,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Tag Archives: News
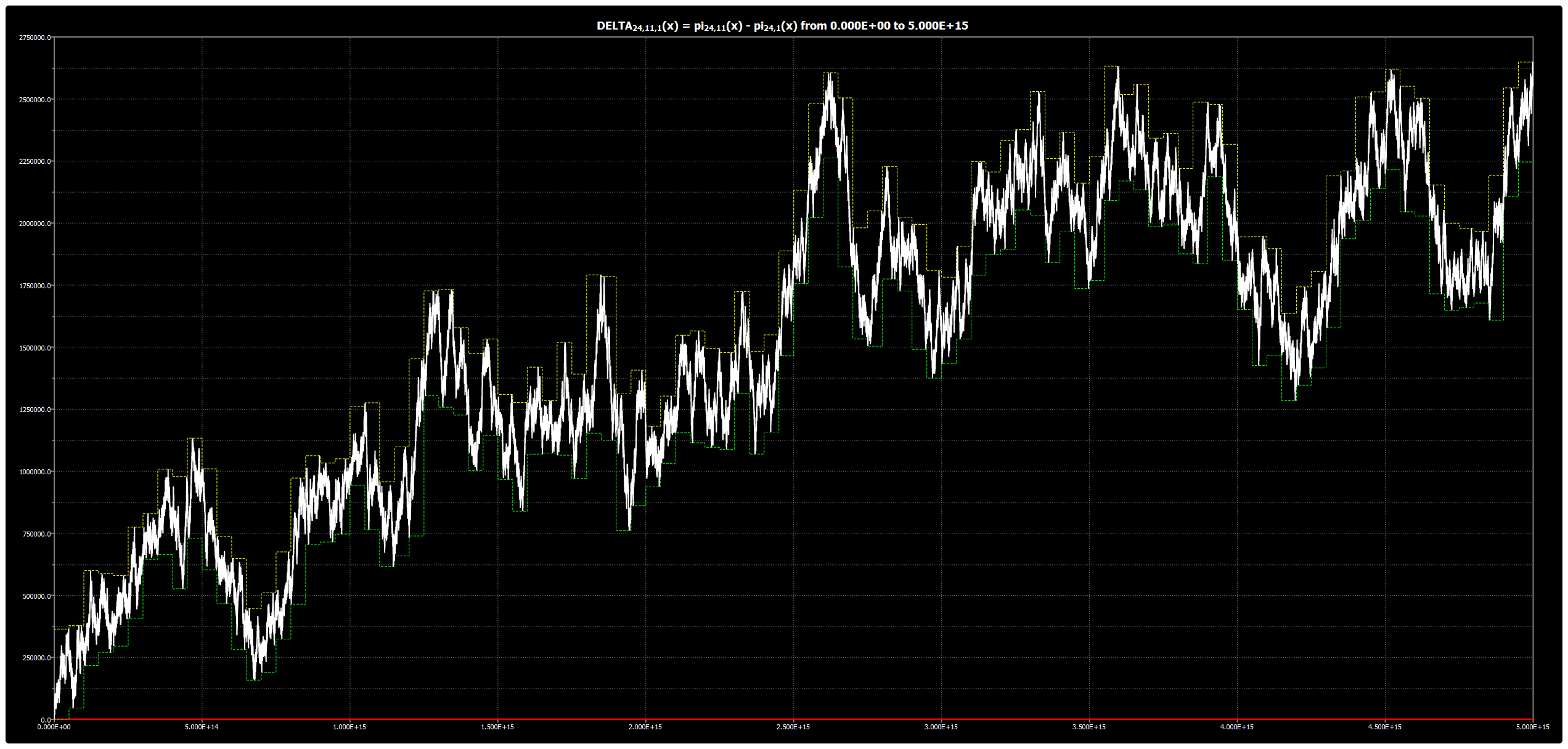
Chebyshev’s Bias: Chart for DELTA{24,11,1}(x)
We are publishing the chart for DELTA{24,11,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
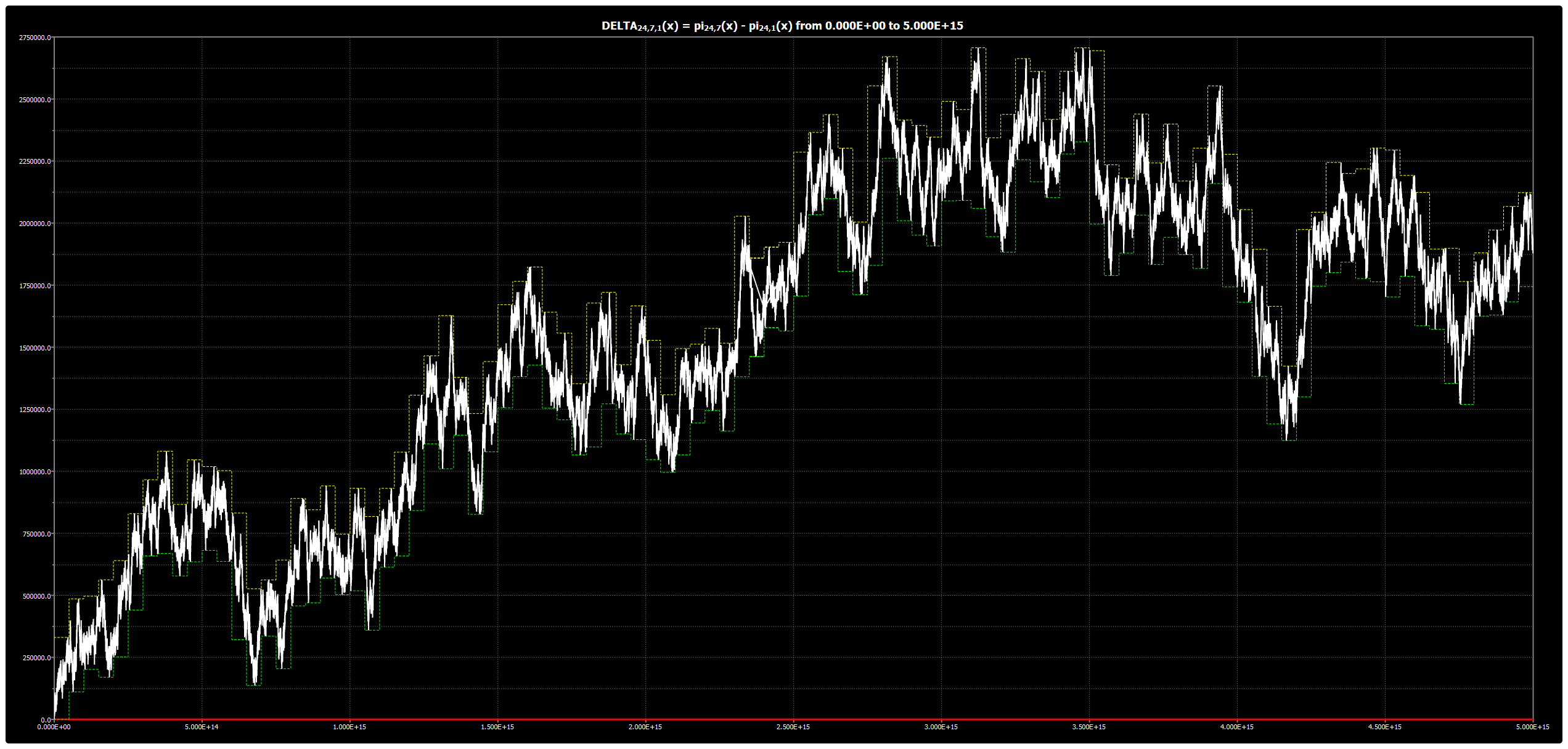
Chebyshev’s Bias: Chart for DELTA{24,7,1}(x)
We are publishing the chart for DELTA{24,7,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{24,5,1}(x)
We are publishing the chart for DELTA{24,5,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{12,11,1}(x)
We are publishing the chart for DELTA{12,11,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{12,7,1}(x)
We are publishing the chart for DELTA{12,7,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{12,5,1}(x)
We are publishing the chart for DELTA{12,5,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{8,7,1}(x)
We are publishing the chart for DELTA{8,7,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{8,5,1}(x)
We are publishing the chart for DELTA{8,5,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{8,3,1}(x)
We are publishing the chart for DELTA{8,3,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{4,3,1}(x)
We are publishing the chart for DELTA{4,3,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.
Chebyshev’s Bias: Chart for DELTA{3,2,1}(x)
We are publishing the chart for DELTA{3,2,1}(x) up to 5*1015 in Chebyshev’s Bias. The chart was obtained using our Chebyshev’s Bias Visualizer.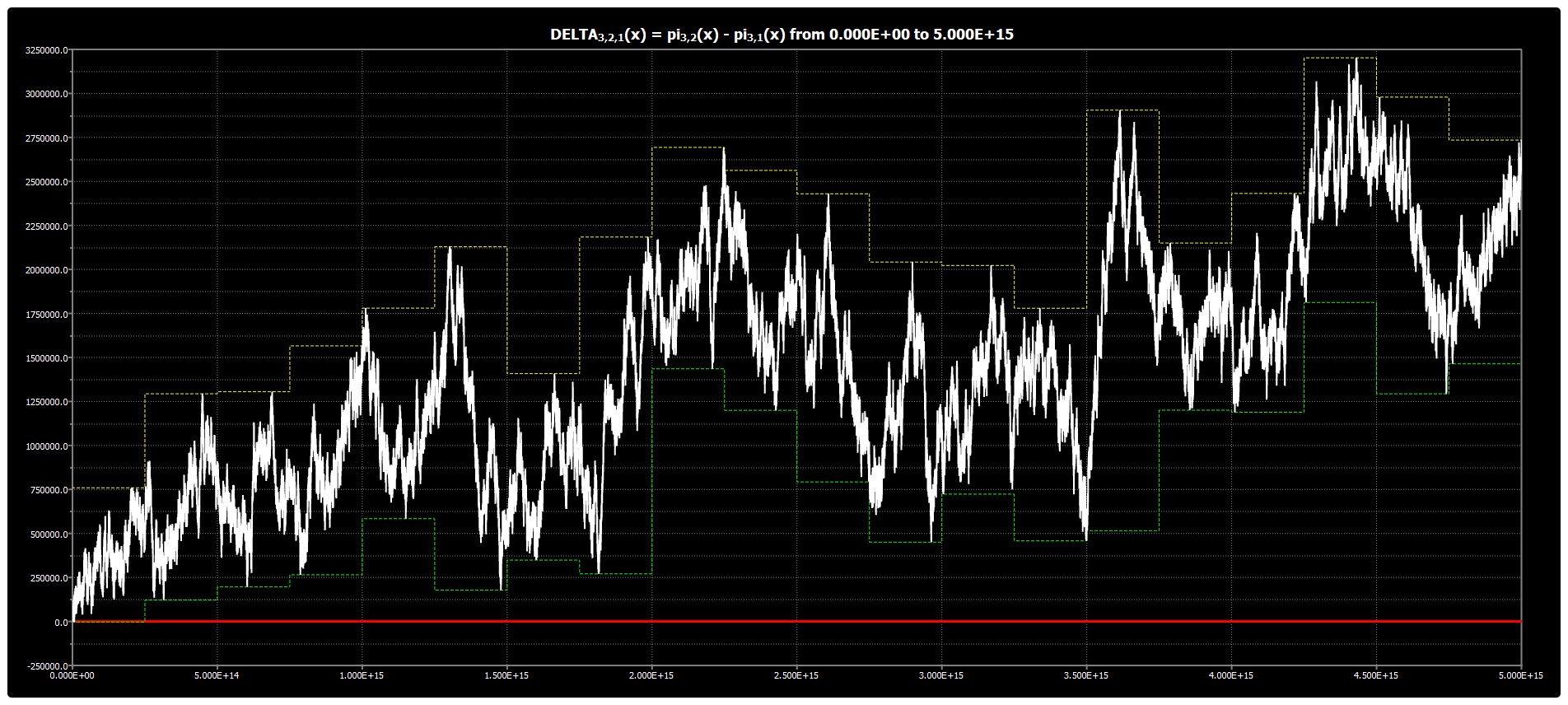
MacOS version of new “Chebyshev’s Bias Visualizer” released
We are releasing the MacOS version for the new “Chebyshev’s Bias Visualizer”. The new version has an improved user interface as well as a number of additional features like chart scrolling and zooming. For your convenience, the executable is released in .app as well as in .dmg versions.
Please, download it through the following link: cbv2_macos64_setup.
The version was tested for MacOS Catalina on a virtual machine only.
Number of Cardan grilles
For my Cryptography classes I wrote a small application that calculates a total number of unique Cardan grilles and generates some of them. You can download it here (Windows 64 bit only!).
I also generated 262144 unique Cardan grilles for a 6×6 square. This is also available for download. Enjoy!
Coupon collector’s problem
For my Probability and Statistics classes I wrote a small application that solves a famous Coupon Collector’s Problem: “A breakfast cereal manufacturer offers a coupon hidden in each package of cereal, and there are K kinds of coupons altogether. The collector wants to have a complete collection of all K coupons. What is the probability P(N,K) that exactly N boxes of cereal will have to be purchased in order to obtain, for the first time, a complete collection of at least one of each of the K kinds of coupons?”
You can download our application here (Windows 64-bit only). The application uses bignum arithmetic and works for any K and N . The solution was also separately confirmed by numerical simulation. Enjoy!