Мы публикуем график для DELTA{24,23,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
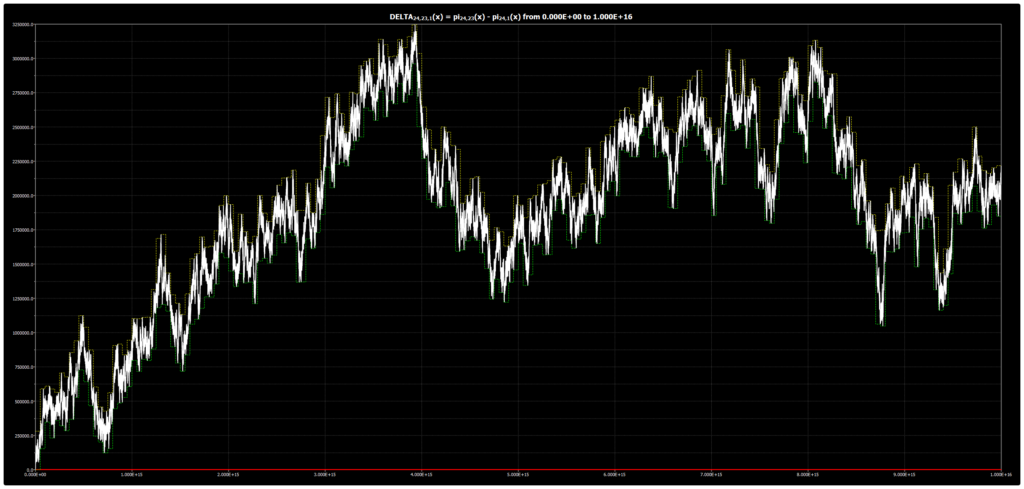

Мы публикуем график для DELTA{24,23,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.

Мы публикуем график для DELTA{24,19,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
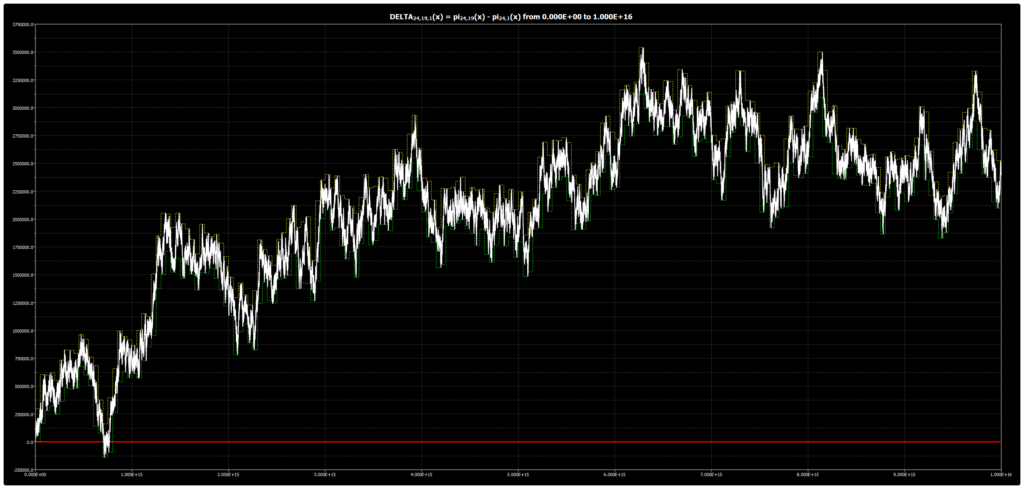
Мы публикуем график для DELTA{24,17,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
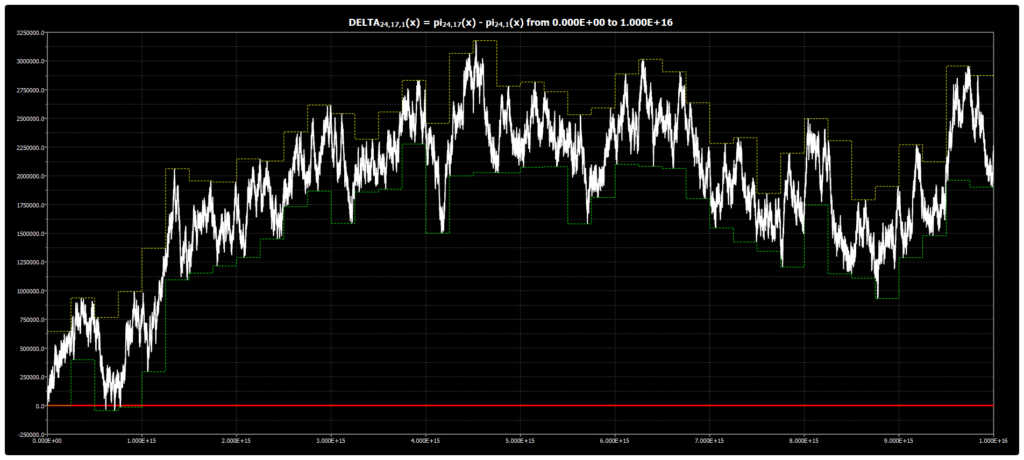
Мы публикуем график для DELTA{24,11,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
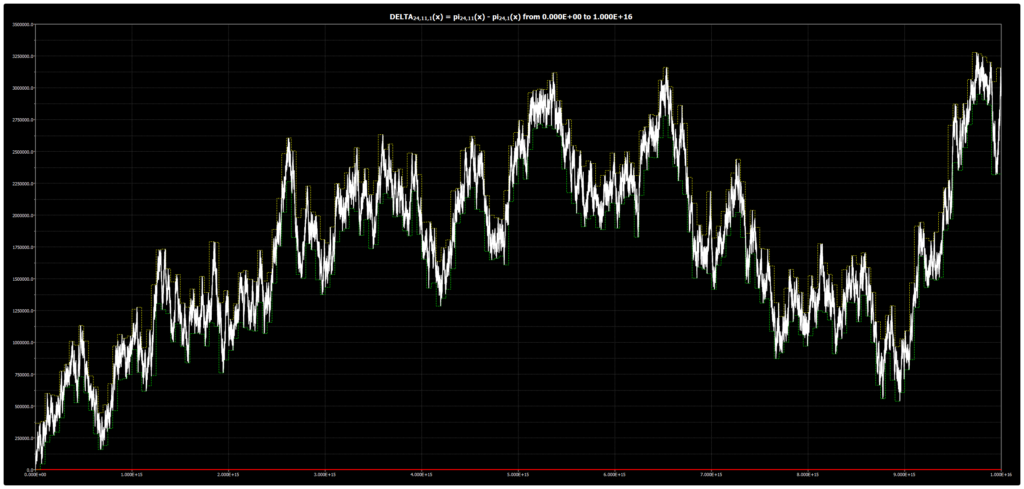
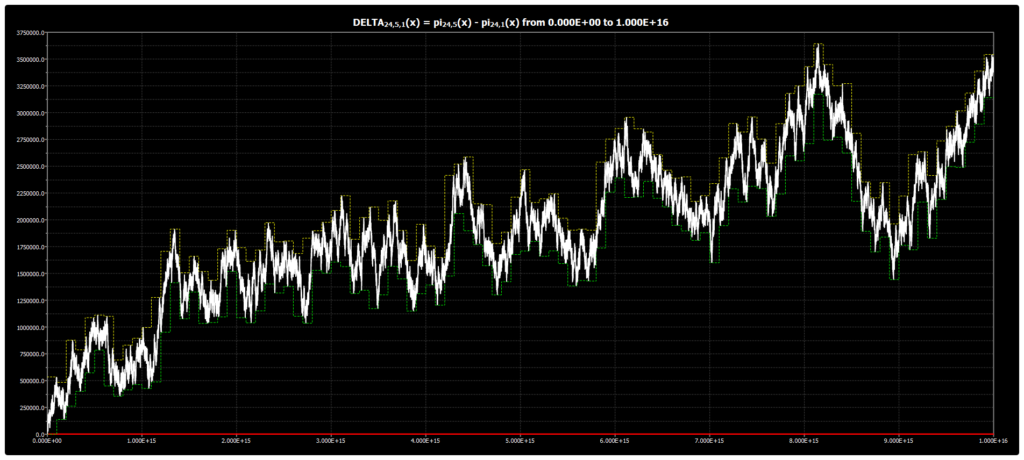
Мы публикуем график для DELTA{24,5,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
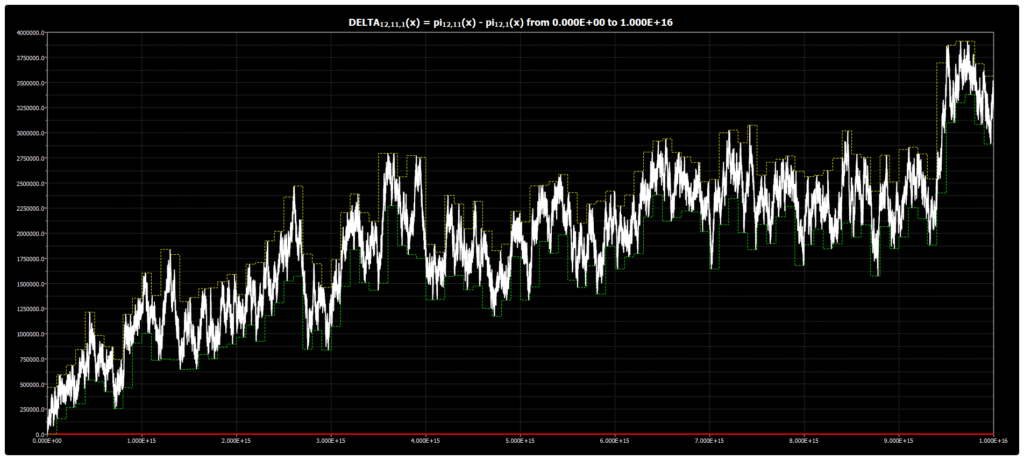
Мы публикуем график для DELTA{12,11,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
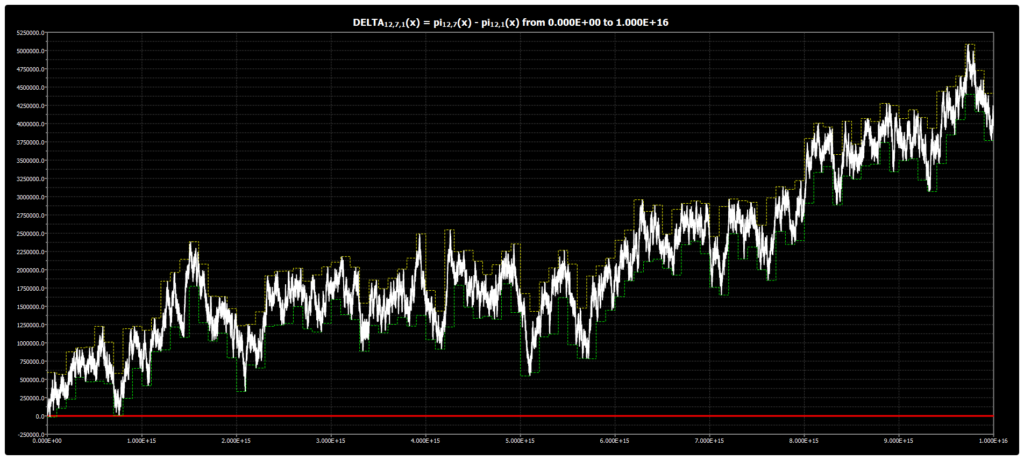
Мы публикуем график для DELTA{12,7,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
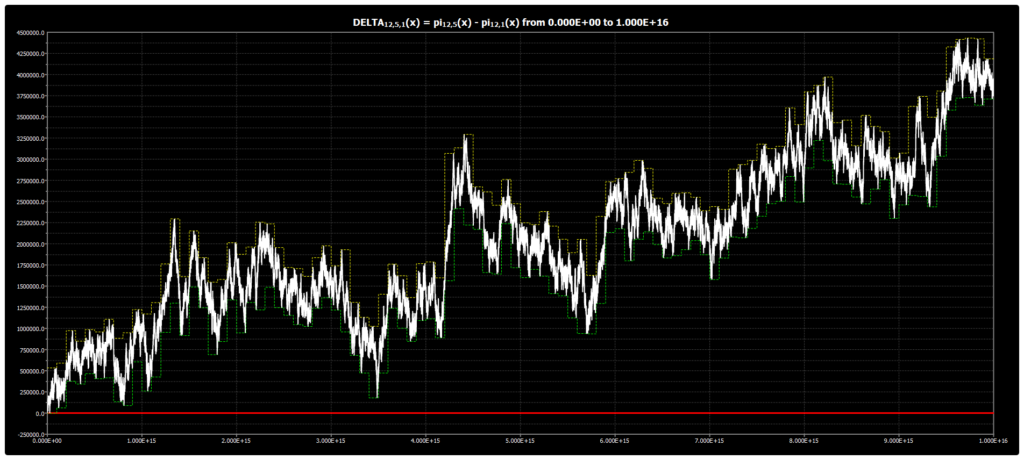
Мы публикуем график для DELTA{12,5,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
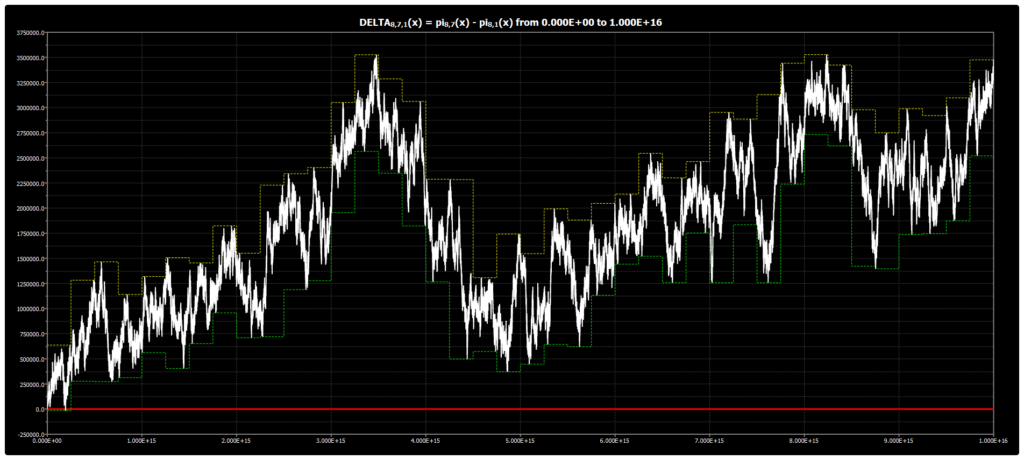
Мы публикуем график для DELTA{8,7,1}(x) до 1016 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
Мы публикуем график для DELTA{24,23,1}(x) до 5*1015 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
Мы публикуем график для DELTA{24,19,1}(x) до 5*1015 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
Мы публикуем график для DELTA{24,17,1}(x) до 5*1015 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
Мы публикуем график для DELTA{24,13,1}(x) до 5*1015 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.
Мы публикуем график для DELTA{24,7,1}(x) до 5*1015 для гипотезы Чебышёва. График был получен с помощью нашей программы Chebyshev’s Bias Visualizer.