Мы публикуем наши первые данные по поведению функции Коллатца для числа 277232917 – 1 (#2 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±4 от него.
Архив рубрики: Новости
Данные по функции Коллатца для 2^74207281 – 1 (#3 мегапростое число)
Мы публикуем наши первые данные по поведению функции Коллатца для числа 274207281 – 1 (#3 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±6 от него.
Данные по функции Коллатца для 2^57885161 – 1 (#4 мегапростое число)
Мы публикуем наши первые данные по поведению функции Коллатца для числа 257885161 – 1 (#4 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±8 от него.
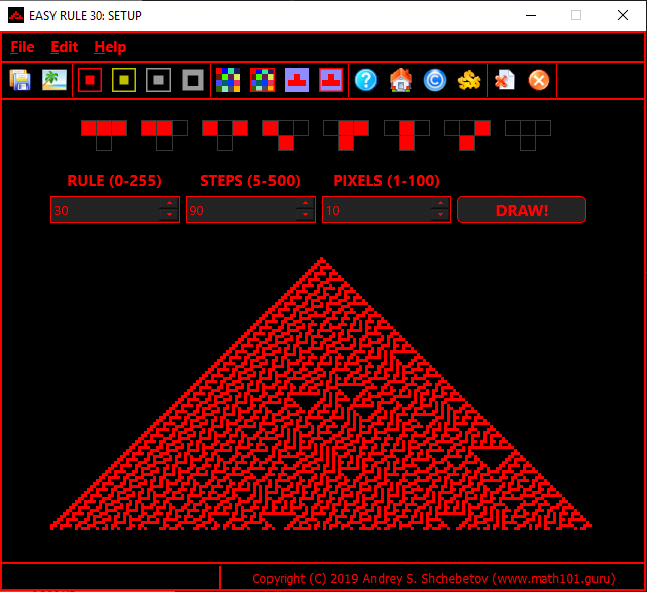
Программа «Easy Rule 30» была обновлена
Наша программа «Easy Rule 30» была обновлена. Вы можете загрузить обновленную версию по следующим ссылкам:
Данные по функции Коллатца для 2^43112609 – 1 (#5 мегапростое число)
Мы публикуем наши первые данные по поведению функции Коллатца для числа 243112609 – 1 (#5 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±10 от него.
Дополнительные данные по функции Коллатца для 2^42643801 – 1 (#6 мегапростое число)
Мы публикуем дополнительные данные по функции Коллатца для 242643801 — 1 (#6 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±12 от него.
Из графика видно, что после достижения максимума скорость падение логарифма функции Коллатца является одной и той же для всех проверенных чисел и приблизительно равна -0.096.
Программа «Easy Rule 30» доступна для загрузки
Наша программа «Easy Rule 30» стала доступна для загрузки.
Пожалуйста, используйте следующие ссылки для загрузки:
Данные по функции Коллатца для 2^42643801 – 1 (#6 мегапростое число)
Мы публикуем наши первые данные по поведению функции Коллатца для числа 242643801 – 1 (#6 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±12 от него.
Разработана программа «Easy Rule 30»
1 октября 2019 года известный американский математик Стивен Вольфрам объявил о начале научного соревнования названного «Wolfram Rule 30 Prizes».
Данное соревнование посвящено решению одной из нерешенных проблем математики в области клеточных автоматов, называемой «Правилом 30».
Последовательность из 19353600 рекордных 288-шаговых отложенных палиндромов опубликована
Наша последовательность из 19353600 рекордных 288-шаговых отложенных палиндромов опубликована в OEIS как A326414.
Эта последовательность начинается с 12000700000025339936491 (числа, найденного Робом ван Нобеленом 26 апреля 2019 года), заканчивается 29463993352000000700020 и содержит все члены, известные на сегодняшний день.
Данные по функции Коллатца для 2^37156667 – 1 (#7 мегапростое число)
Мы публикуем наши первые данные по поведению функции Коллатца для числа 237156667 – 1 (#7 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±26 от него.
Данные по функции Коллатца для 2^32582657 – 1 (#8 мегапростое число)
Мы публикуем наши первые данные по поведению функции Коллатца для числа 232582657 – 1 (#8 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±71149323674102624414 от него.
Данные по функции Коллатца для 10223×2^31172165 + 1 (#9 мегапростое число)
Мы публикуем наши первые данные по поведению функции Коллатца для числа 10223×231172165 + 1 (#9 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±4 от него.
Данные по функции Коллатца для 2^30402457 – 1 (#10 мегапростое число)
Мы публикуем наши первые данные по поведению функции Коллатца для числа 230402457 – 1 (#10 известное мегапростое число) и его 2 нечетных соседей, расположенных на расстоянии ±2 от него.
Найдена последовательность рекордных 288-шаговых отложенных палиндромов
26 апреля 2019 года Роб ван Нобелен нашел 23-значное 12000700000025339936491 — первое, которому необходимы рекордные 288 шагов для того, чтобы стать 142-значным финальным палиндромом. Предыдущий рекорд (261 шаг) был установлен в 2005 году.
Мы расширили эту последовательность с одного числа до 19353600 чисел. Таким образом, эта последовательность включает все известные в настоящии время 288-шаговые отложенные палиндромы.
Все результаты внесены в Онлайн Энциклопедию Целочисленных последовательностей и будут опубликованы в ближайшее время.