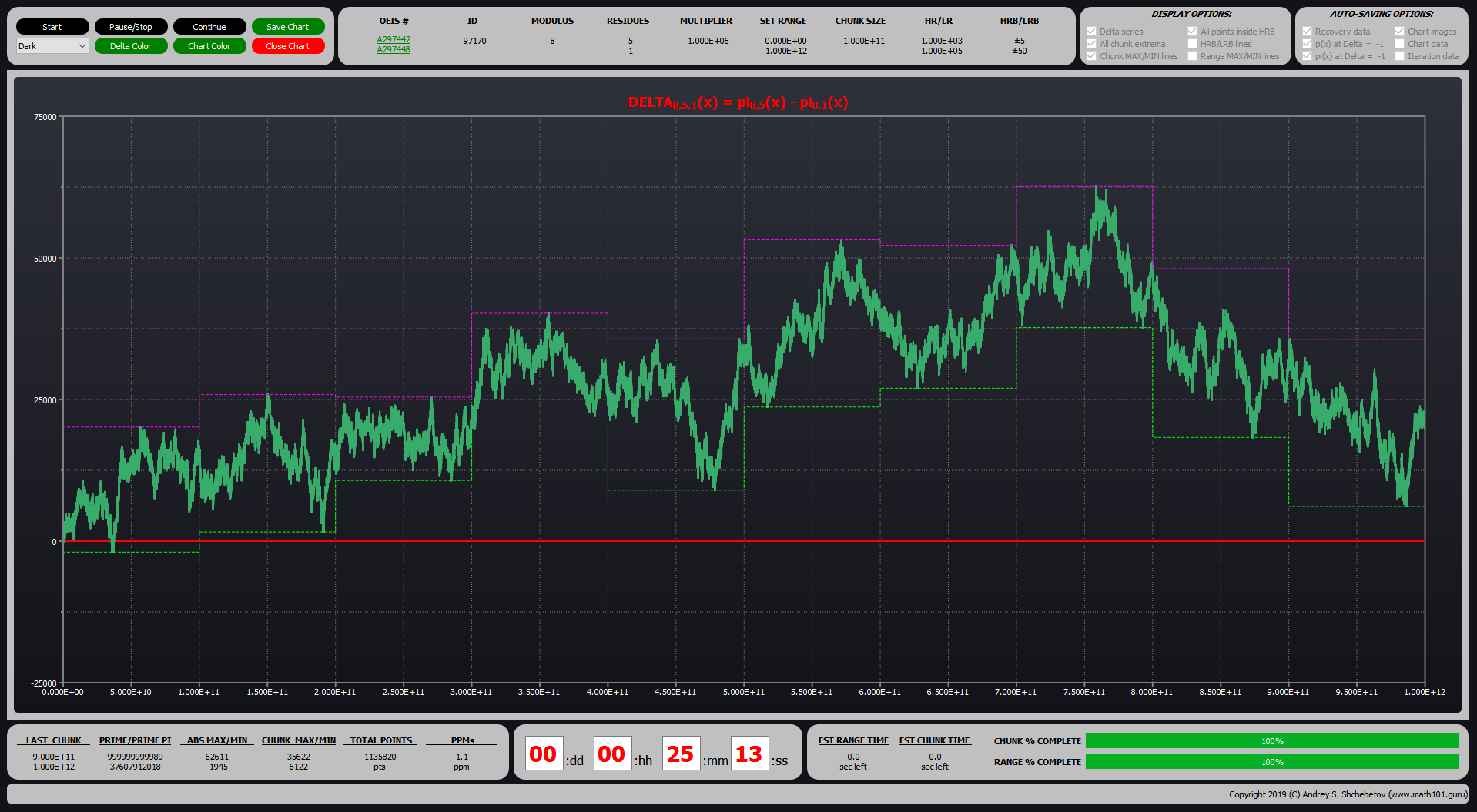
Мы выпускаем новую версию «Chebyshev’s Bias Visualizer» для MacOS. Новая версия имеет улучшенный пользовательский интерфейс и новые функции, включающие возможности прокрутки и изменение масштаба графика. Для удобства пользователей, приложение выпускается как в виде .app так и в виде .dmg.
Вы можете скачать программу по следующей ссылке: cbv2_macos64_setup.
Данная версия была протестирована на MacOS Catalina только на виртуальной машине.